前置きが長くなりましたが、ここでは折り紙作品に対して批評することを真面目に考えたいと思います。
最近になって、笠原氏をはじめとする雄弁な著作が出版されるようになってきましたが、これまで多くの批評的性格を持った文章は、創作を中心とする活動家の手によるものです。このような立場からの客観的な批評は難しく、著者自身、これまで創作を発表することでのみ折り紙と係わってきたひとりです。しかしながら、多少なりとも作品に対する批評を行うためには、その世界に関する知識を持っていることが必要であり、更になによりもある作品（作家）に対する感動が無ければならないでしょう。その意味でこれらを満たしている人々は、つまり自身が創作家となり得た人々であったこともまた事実です。それを承知でここでは折り紙を折らない人の折り紙に対する係わり方を考えることにもなると思われます。
それでは次に折り紙の世界に既に存在する幾つかの価値観について考えていきたいと思います。以下箇条書にまとめますと、
ここに紙があります。紙は折られるものです。その紙が便箋なら三つ折り、四つ折りすると封筒に収まることに気がつくでしょう。薬包紙包みは中の薬が飛び出さないように、また小さく持ち運び便利になります。大きなポスターは丸めるとやはり運ぶのに楽です。紙は折られることによって（折ると曲げるを区別するかしないかはそれ自身テーマとなるところですが）様々に形を変え目的に適応することができる素材です。そんななかでいわゆる折り紙は紙が折られることによって何かの形を示す作業、つまり造形が目的となったものと言えるかもしれません。＊１
もう一つはこれとは逆に、造形を目指して紙という素材を選び、更に手法として折ることを選ぶに至るとき初めの造形の目標はどんなものだろうかと考えてみる方法です。便箋に例えれば、中に書かれたものが保存されなくてはいけないわけですから、同じように封筒に収まるにしても切ってはならないし広げたときに文字が読み取りにくくなるほど複雑に折ってもいけません。ポスターの場合となると描かれた絵が折り線によって損なわれないように丸めるという手法が適切に選びだされたと見ることができるでしょう。しかし一度造形が目指されると折るという手法にこだわる意味はこんなに単純にはいきません。出発点の目標に当たりを付ける意味でも、一つ目の考えをもう少し進めてみる必要があります。
一つ目の考え方はもう少し強い言い方をすれば、紙という素材に出会ったとき折ることがもっとも自然な行為ではないかと言うことです。そうして折り始めた人は様々な発見を喜びます。折り紙の魅力の一つが折る工程そのものであることは多くの人の認めるところでしょう。ひと折りひと折りで規則的にあるいは思いがけなく形が変化していく様は、自分の指で折っているにも拘らず何か自然を観察しているような気がしてくるものです。折っているうちに何かの形に見えてきて、更にそれらしい形にしようと工夫を楽しみます。創作者は、このような折るという手法の持つ魅力と最終的な形（造形）とを同時に認識します。そして少し意地悪く言えば、同時に体験するがゆえに混同します。表現として三次元的に示される折り紙の作品は、少なくとも作者にとっては四次元的に認識されているはずです。この感覚はテーマとして物の形を示そうとしているにも拘らず、一枚不切なる制約（表現を目指すには余りに強い）を掲げさせるものと思います。このような視点に立てば作者の意図が表現にあるのか、手法そのものにあるのかが批評の対象となってくるでしょう。実際は、両者の力点が様々にバランスして折り紙的（四次元的な）と言えるような世界が出来てくると思われます。一枚不切にこだわることは、折り紙的であろうとするときのもっとも易しい（たとえ技術的な壁がどんなに大きくとも）規準であると理解します。つまり、「これは一枚の紙から出来ています。」という言葉が、事実が紙の変化してゆく動的なイメージを（たとえ極めて不正確であっても）鑑賞者に想像させて、作者の認識に近づけるきっかけを与えます。しかしながら、真に鑑賞者に想像の努力を促すものはこのような事実でしょうか。筆者は最終的に表現された形であると考えています。
折り紙において一枚不切という制約に対する議論はまだまだ続けていかなくてはなりませんが、とりあえず全体を概観する意味で、次は造形的な意味について考えてみたいと思います。
話が抽象的になってしまいましたが、ここでの議論は漠然と認められてきた価値観を評論する切り口を模索するものです。これをお読みになった方の御意見をお寄せ下さい。誌上討論や座談会のような形式も考えたいと思います。
＊１伝統的に折り紙と呼ばれるものの中で紙飛行機は、機能面での評価が可能であり、目標が比較的容易に定義されます。この種の作品は今後折り紙の遊戯性と関連させて考えることになると思われます。
以上のことを念頭におきながら”折り紙的”と言うことについて造形的な立場から考えてみたいと思います。
折り紙がどんなものをテーマに選んできているでしょう。ある種のデータを示さなければならないところですがそれを割愛しても、テーマは実際に存在するかあるいはなにか別の表現手段によって示されたことのあるものだということは認められるところでしょう。言い直せば、既に一般的な共通の概念が成立しているものです。手法として制約の強い表現法にとってこれは、宿命的なものとも考えられます。このことを筆者は悲観しているのではありません。そこには、知識や感覚を共有するものの間で成立するパロディー感覚や見立ての面白さが生じます。このような面白さは、幾つかの表現手段（似顔絵、影絵など）にとって独特のものであって、折り紙による造形もその仲間にはいると考えられるでしょう。そこで、作家はいろいろな表現法を考えます。
ある作品、例えば”象”という作品があったときそれは”折り紙による象”と鑑賞されるものです。折り紙である以上折ろうとすれば折れるものでしょう。そして、折ってみるときにすることは最終的な造形を思い浮かべることです。これは先に述べたこととは逆のことで、鑑賞者が表現された形をどのように認識しているかが四次元的な捕らえられ方を左右します。その象が、「インド象ではなく、なるほどアフリカ象をイメージして作られている」とか、「牙が表現されていたが、なるほどこう折れば牙が折り出せるのか」などとやるわけです。表現されるものが共通の概念を前提としているなら、上述の例でどちらの意識がより一般的でしょうか。筆者は後者のような気がしますが、前者が共通の概念として成立していれば作品をより楽しめることは確かでしょう。ここに、作品を評論することの一つの意味が生じてくると考えられます。
作品が折り紙であることを思い出してみる必要があります。折り紙の作品の持つ情報の一つが最終的な形であるなら、もう一つの大切な情報は、それが折ることで形作られていると言うことです。折らない鑑賞者には、例えば、折って作られた象は（事実折って作ったのだから）必ず折って作られていると認識されるでしょうか。鼻は、折っているように見えますか？ 牙はどうでしょう、足は、それらすべては一枚の紙から折り上げられていることが理解されますか？ この問題は極めて重要です。前回、あるいは前々回の議論の中でこれを折ること無しに体験する術は、知識でありました。しかし、もし、折って作られた形がそれ自身で折って作られていることを明示しているなら、手法と造形を非常に効果的に同時体験することが可能だと思われるからです。
折り紙の世界にどっぷり漬かった筆者にとって、このことを想像してみることはもはや容易ではありません。鶴の頭のたった１工程前が真っすぐな角であることの面白さが理解されるでしょうか。正方形でも長方形でも９０度の角は、４つしか在りません。５つ以上の角があれば必ず１つ以上は１８０度（つまり辺）から折り出さなくてはいけません。当然、紙の重なりは倍になります。それを見付けて折っていることを信じることができるでしょうか。恣意的に彩色されていない紙を用いて３色以上の色分けが美しい作品が２枚以上の紙を用いる必然性を理解してもらえるでしょうか。少なくとも鶴の頭に代表される部分については、折られていることとそれが何かに見立てられることを同時に体験できると信じます。第２回で議論した、”手法として折ることを選んだ立場”で考えるなら、この同時体験を期待することこそ造形の目標であるように思われます。折るという手法の独自性は、折るという手法とそれによって得られる（発見される）形（色分け）が何かに見立てられる（美しい）ことを同時に理解されたとき極めて効果的に発揮されるでしょう。正方形からそれが形作られる様を正確に理解することが難しいにしても、折って形が作られていることを本当に信じさせてくれるような発見がそこにあれば、一枚であるとか、不切であると言ったような知識による理解補助とは比べものにならない感動が得られるものと期待します。
折るという手法で得られる（発見される）形に一体どれほどの多様性があるものでしょう。それを考える意味で次回は幾何学的な側面から考えてみます。
もう一つは、幾何学の問題を折り紙で表現するやり方です。例えば、有名な任意角の三等分（阿部氏）を一つの作品としてみることです。このためには、前回述べた「造形に対する前提となる共通概念の必要性」と同様に幾何学的な背景を必要としそうです。
具体的に見てみましょう。
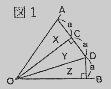
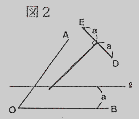任意角の３等分という問題は、ギリシャの三大難問の一つで、「直線定規とコンパスだけを用いて任意の角の３等分をせよ」というのが本来の問いの形です。では、それが折り紙で出来たということはいったいどういうことなのでしょうか。図の１を見てください。今任意な角AOBについて点C，Dがそれぞれこの角をに３等分する直線を与えています。（△XYZがすべて合同）このような点C，Dは、次のように求めることが出来ます。図の２のようにOB
からaだけはなれたところにOBに平行な直線lを考え太い線で示したT定規をDがl上にかつEがOA上に、かつ柄に当たる直線がOと重なるように置けば、図の１になることが判ります。このようなT定規を使って良いなら難問とは呼ばれなかったわけです。１）
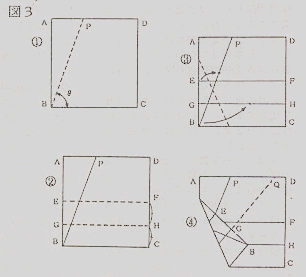では、折り紙は何をしたのかと言うことを考えてみなければなりません。実際の折り手順は図の３に示したものです。２） 図の１が作図されています。もとより、折り紙は定規もコンパスも使用しないわけですから長年の難問を解き明かしたわけではありません。実は、コンパスと直線定規では不可能であることは既に証明されています。つまり「折るという作業のみで（都合の良い道具を使うこと無しに）コンパスと直線定規では得られない作図が可能であることを示した」とは、折り紙独特の幾何学の存在を示したことになります。３）
折ることに潜む独特の幾何学が持つ自然さが、私達がボールの弾道を見て放物線という知識を持たずとも自然な飛び方を感じ取れるほどに自然に感じられて、折り紙の作品を見た時、折ることによって形造られていることを理解させてくれるなら、折るという手法を造形の手段として用いた意味は更に大きなものとなると思われます。
１） 「数学ふしぎ・ふしぎ」新潮文庫 矢野健太郎著
２） 「おりがみ新世紀」笠原邦彦著
３） 「創造性の文化と科学」伏見康治編著 の藤田文章氏の章は、このあたりに興味のある人は是非読んでみてください。
そのほか、ピーターエンゲルがフラクタル幾何学をその著書の中で大きく取り上げていたのは興味深い。
長々と続けてきた抽象的な議論はそろそろおしまいにしなくてはいけません。回を改め、具体的な作家や作品についての批評的な文章を書かせていただくことになるでしょう。これまで、これをお読み戴いた方で、批評することの必要性を感じて戴ければ幸いです。この新聞をお読みになっている方は恐らく、折り紙が大好きな方々でしょう。大好きと言えるような作品や作家について、語ってみてください。どんな小文でも構いません。投稿は何時でも募集しています。多くの人の折り紙作品に対する思いが、折り紙批評体系なるものを形造っていくものと思います。