節足法について考えてみる
節足動物の体節構造を折り紙設計として再現する設計法
[923] 節足動物 投稿者:めぐろ 投稿日:2003/01/22(Wed) 03:0
[924] 節足動物 投稿者:めぐろ 投稿日:2003/01/22(Wed) 03:12
[927] ショウジョウバエ 投稿者:めぐろ 投稿日:2003/01/22(Wed) 03:36
[928] 展開図上の帯領域と節足動物の体節との対応 投稿者:めぐろ 投稿日:2003/01/22(Wed) 04:05
[942] 節足法について考えてみる(1) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 17:44
[943] 節足法について考えてみる(2)、一体節だけ設計してみる 投稿者:めぐろ 投稿日:2003/01/25(Sat) 18:38
[944] 節足法について考えてみる(3) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 19:41
[945] 節足法について考えてみる(4) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 20:33
[946] 節足法について考えてみる(5) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 21:19
[947] 節足法について考えてみる(6) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 22:57
[948] 節足法について考えてみる(7) 投稿者:めぐろ 投稿日:2003/01/25(Sat) 23:38
[949] 節足法について考えてみる(8) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 00:25
[950] 節足法について考えてみる(9) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 01:27
[951] 節足法について考えてみる(10) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 01:43
[952] 節足法について考えてみる(11) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 17:31
[953] 節足法について考えてみる(12) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 21:30
[954] 節足法について考えてみる(13) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 21:30
[955] 節足法について考えてみる(14) 投稿者:めぐろ 投稿日:2003/01/26(Sun) 22:01
[956] [955]の写真 投稿者:めぐろ 投稿日:2003/01/28(Tue) 02:14
[988] 「体節法」について 投稿者:みるかし姫@ごぶさた 投稿日:2003/02/23(Sun) 09:15
[990] みるかし姫さん 投稿者:めぐろ 投稿日:2003/02/23(Sun) 19:5
[991] クモ折紙 投稿者:めぐろ 投稿日:2003/02/23(Sun) 21:20
[992] クモの体節構造について 投稿者:みるかし姫 投稿日:2003/02/23(Sun) 22:32
[993] ムカデなど 投稿者:めぐろ 投稿日:2003/02/23(Sun) 23:05
[994] ムカデのツラ 投稿者:みるかし姫 投稿日:2003/02/23(Sun) 23:17
[995] クモの体節構造 投稿者:めぐろ 投稿日:2003/02/23(Sun) 23:29
[997] クモのからだ 投稿者:めぐろ 投稿日:2003/02/24(Mon) 00:44
[998] 昆虫とクモ類の体節の相同性 投稿者:みるかし姫 投稿日:2003/02/24(Mon) 18:41
[1000] 昆虫とクモ類の体節の相同性2 投稿者:みるかし姫 投稿日:2003/02/24(Mon) 21:24
[1001] 発生学と折り紙 投稿者:みるかし姫 投稿日:2003/02/25(Tue) 10:20
[1002] ムカデのアップ 投稿者:めぐろ 投稿日:2003/02/26(Wed) 00:59
[1003] みるかし姫さん 投稿者:めぐろ 投稿日:2003/02/26(Wed) 11:45
[1011] みるかし姫さん 投稿者:めぐろ 投稿日:2003/03/13(Thu) 00:59
BACK TO INDEX
ようこそ、折紙のホームページへ


 複数の体節を連続させた構造を設計するにはこの図のように、展開図上で、適当に体節の帯領域を積み上げます。なお、ここの図は。歩脚と鰓脚の正方形領域は面倒なので省略していますが、実際には[943] の図の一番下のように体節に切れ目が入って、そこに正方形領域が詰め込まれた状態になっています。
複数の体節を連続させた構造を設計するにはこの図のように、展開図上で、適当に体節の帯領域を積み上げます。なお、ここの図は。歩脚と鰓脚の正方形領域は面倒なので省略していますが、実際には[943] の図の一番下のように体節に切れ目が入って、そこに正方形領域が詰め込まれた状態になっています。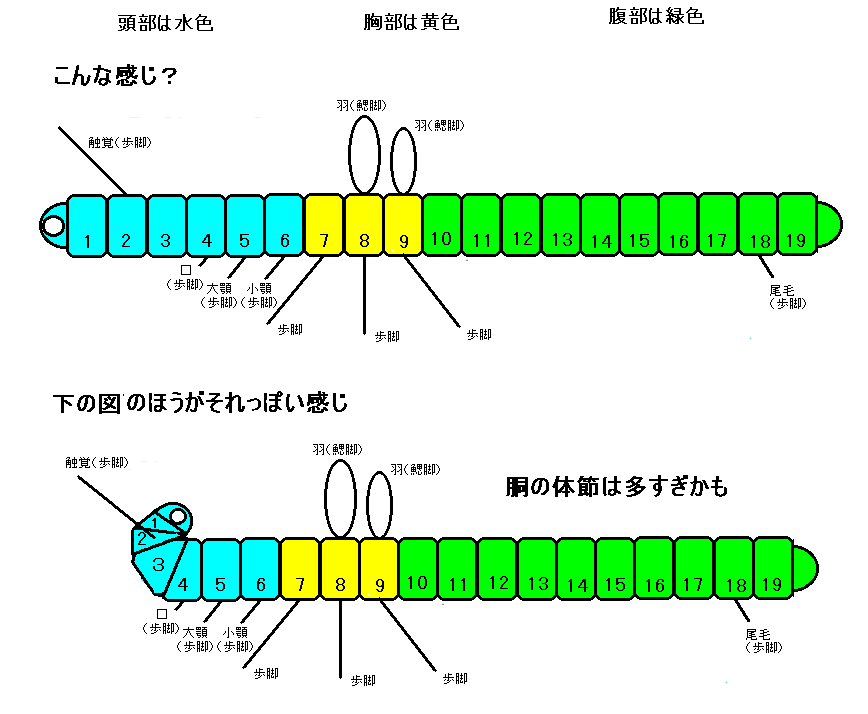


http://screammachine.tripod.co.jp/about.htm