クモ(PART 1)
節足法によるクモ(足長=8、9)の設計実例
[1035] クモ 投稿者:めぐろ 投稿日:2003/03/18(Tue) 12:39
[1037] クモ2 投稿者:めぐろ 投稿日:2003/03/18(Tue) 19:05
[1039] クモ3 投稿者:めぐろ 投稿日:2003/03/18(Tue) 19:14
[1040] クモ4 投稿者:めぐろ 投稿日:2003/03/18(Tue) 19:42
[1041] クモ5 投稿者:めぐろ 投稿日:2003/03/18(Tue) 20:18
[1047] クモ6 投稿者:めぐろ 投稿日:2003/03/20(Thu) 02:51
[1048] ピタゴラス数 投稿者:めぐろ 投稿日:2003/03/20(Thu) 03:33
[1049] クモ7 投稿者:めぐろ 投稿日:2003/03/20(Thu) 05:19
[1050] クモ8 投稿者:めぐろ 投稿日:2003/03/20(Thu) 05:31
[1055] みるかし姫さん 投稿者:めぐろ 投稿日:2003/03/21(Fri) 00:25
[1090] クモ(9) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 14:57
[1091] 8-1-8系 投稿者:めぐろ 投稿日:2003/03/23(Sun) 15:30
[1190] クモ(10) 投稿者:めぐろ 投稿日:2003/04/07(Mon) 02:16
[1191] 蛇腹の方形領域を削ったパターン(1) 投稿者:めぐろ 投稿日:2003/04/08(Tue) 02:49
[1192] クモ(11) 投稿者:めぐろ 投稿日:2003/04/09(Wed) 00:31
[1197] クモ(12) 投稿者:めぐろ 投稿日:2003/04/09(Wed) 20:09
[1198] クモ(13) 投稿者:めぐろ 投稿日:2003/04/09(Wed) 20:12
[1199] クモ(14) 投稿者:めぐろ 投稿日:2003/04/09(Wed) 20:33
[1201] クモ(15) 投稿者:めぐろ 投稿日:2003/04/11(Fri) 02:09
[1202] クモ(16) 投稿者:めぐろ 投稿日:2003/04/11(Fri) 03:26
[1209] クモ(17) 投稿者:めぐろ 投稿日:2003/04/14(Mon) 13:55
[1210] くも(18) 投稿者:めぐろ 投稿日:2003/04/14(Mon) 14:27
[1220] クモ(19) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 01:09
[1221] クモ(20) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 01:15
[1222] クモ(21) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 01:47
[1223] クモ(22) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 02:01
[1224] クモ(23) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 02:19
[1225] クモ(24) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 02:29
[1226] クモ(25) 投稿者:めぐろ 投稿日:2003/04/19(Sat) 16:22
[1229] クモ(26) 投稿者:めぐろ 投稿日:2003/04/20(Sun) 15:29
[1230] クモ(27) 投稿者:めぐろ 投稿日:2003/04/20(Sun) 15:32
BACK TO INDEX
ようこそ、折紙のホームページへ
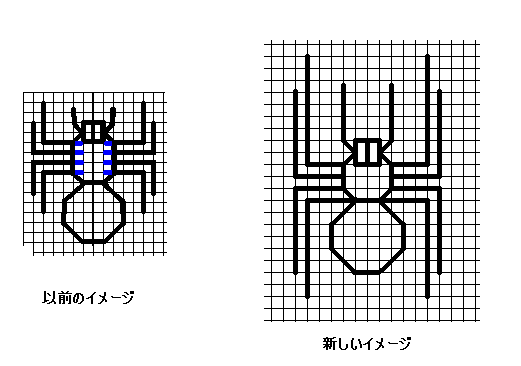
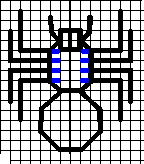 大まかな設計前イメージはこんな感じ
大まかな設計前イメージはこんな感じ
 大まかな設計前イメージはこんな感じ
大まかな設計前イメージはこんな感じ
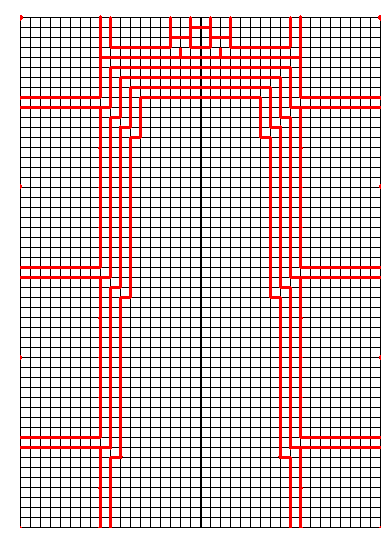

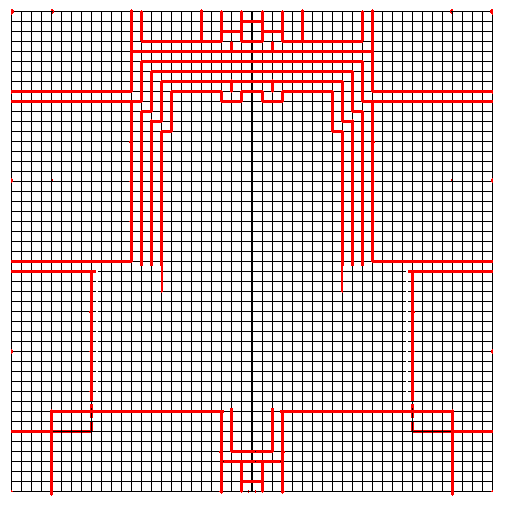
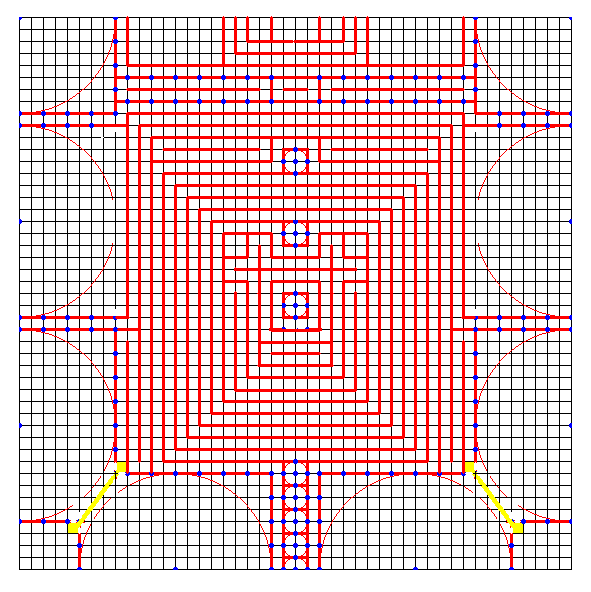
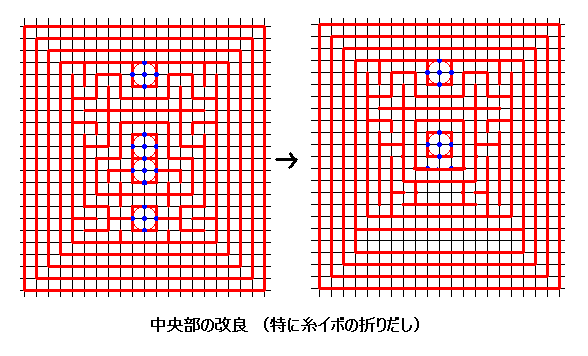
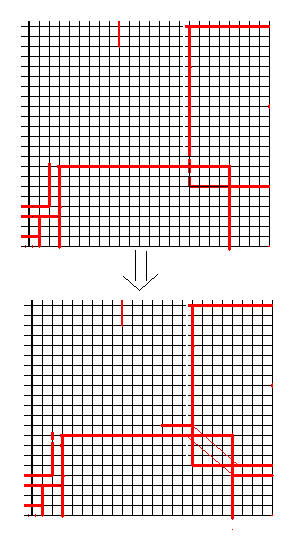 左図の上側は、[1041] のクモ5の図下側に方形領域が干渉しているところをとり出したものである。これは長さ8の足の方形領域が2つあって、それらが干渉しているわけであるが、さらにこの2つの足の領域の間には幅1の帯領域も入るので、実際に折れるようにするには、とりあえず左図の下側のように変形してみるとよい。
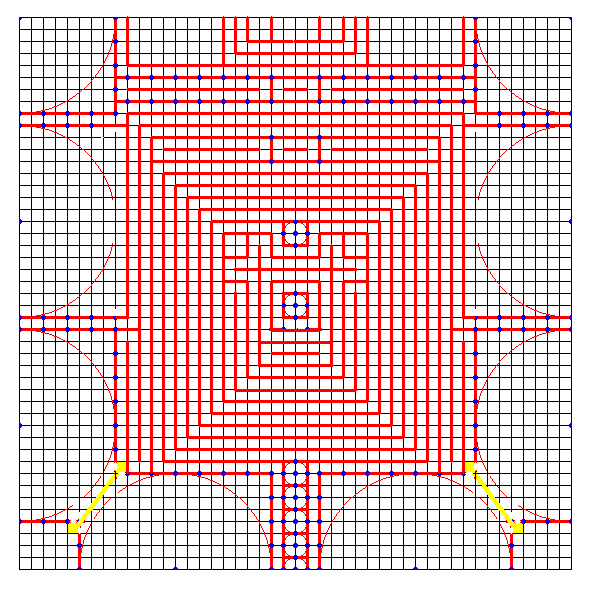
左図の上側は、[1041] のクモ5の図下側に方形領域が干渉しているところをとり出したものである。これは長さ8の足の方形領域が2つあって、それらが干渉しているわけであるが、さらにこの2つの足の領域の間には幅1の帯領域も入るので、実際に折れるようにするには、とりあえず左図の下側のように変形してみるとよい。 [1047]のクモ6 の下図でも一応折れるが、折りにくい等の問題があるので、新たに探したパターンが、ここに示した左図。
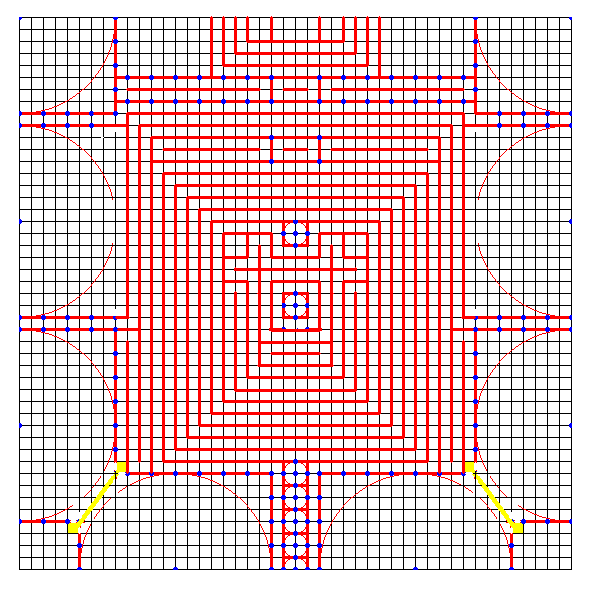
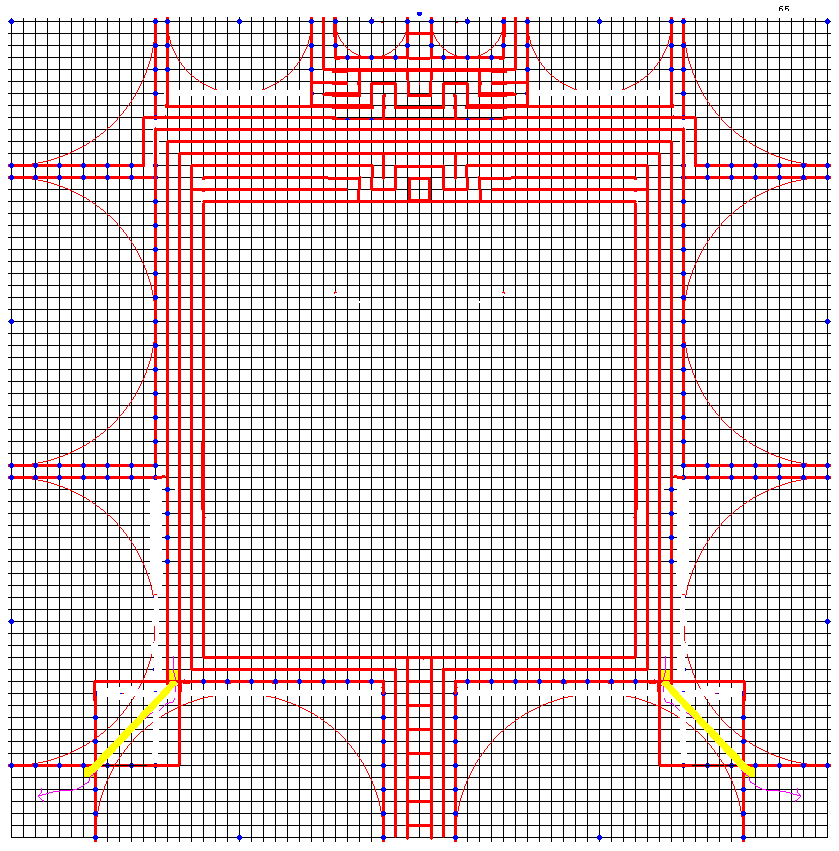
[1047]のクモ6 の下図でも一応折れるが、折りにくい等の問題があるので、新たに探したパターンが、ここに示した左図。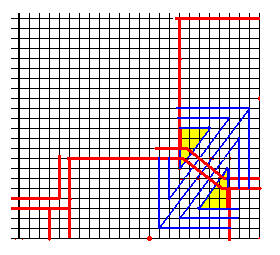 [1049] の図の一部がずれていたので訂正
[1049] の図の一部がずれていたので訂正

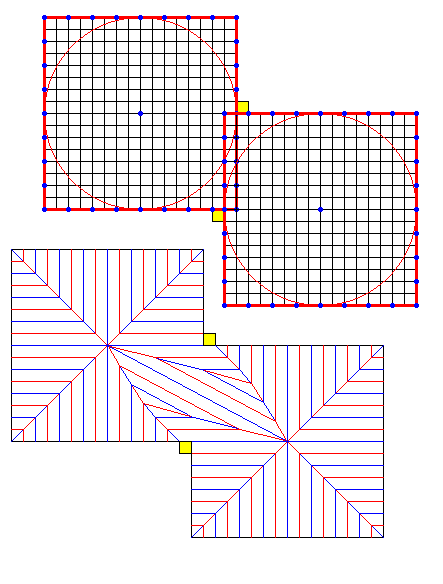
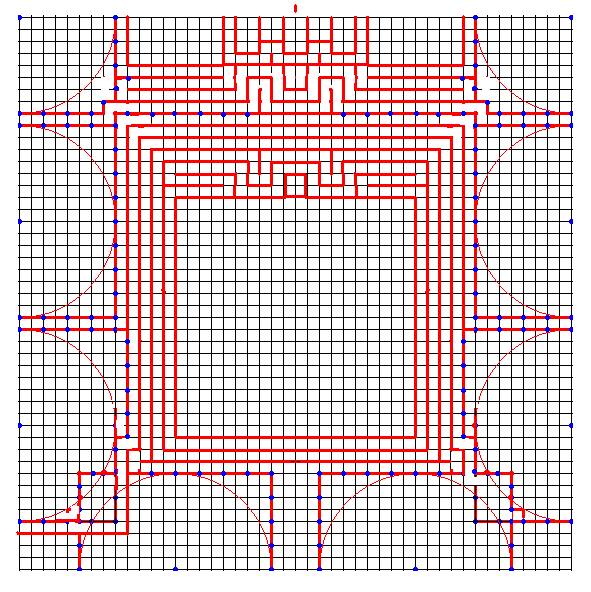
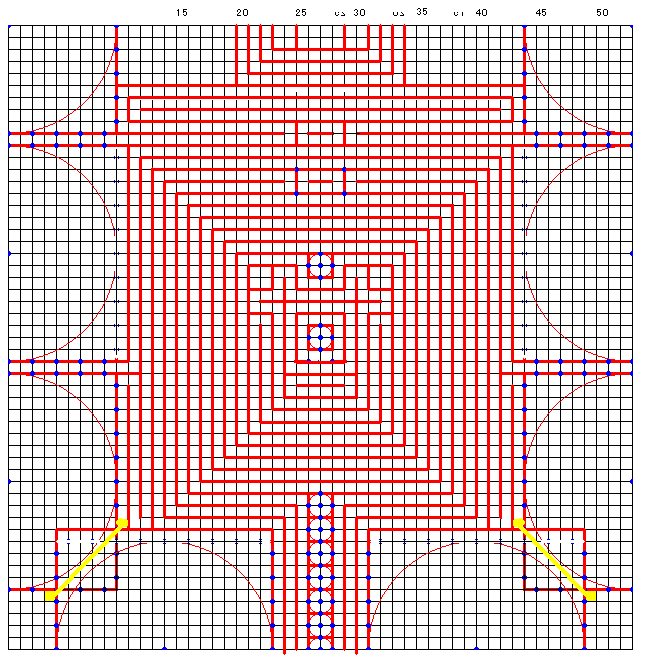
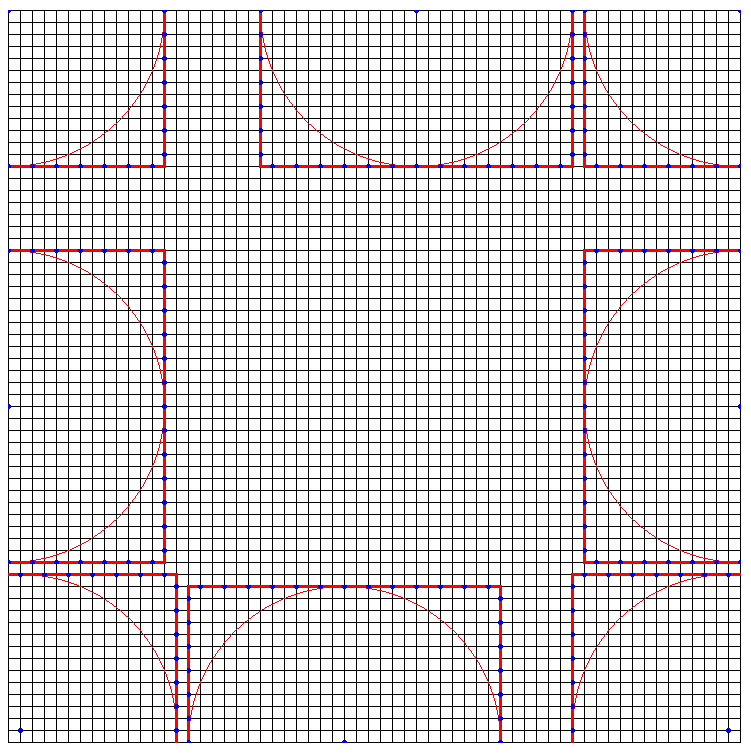
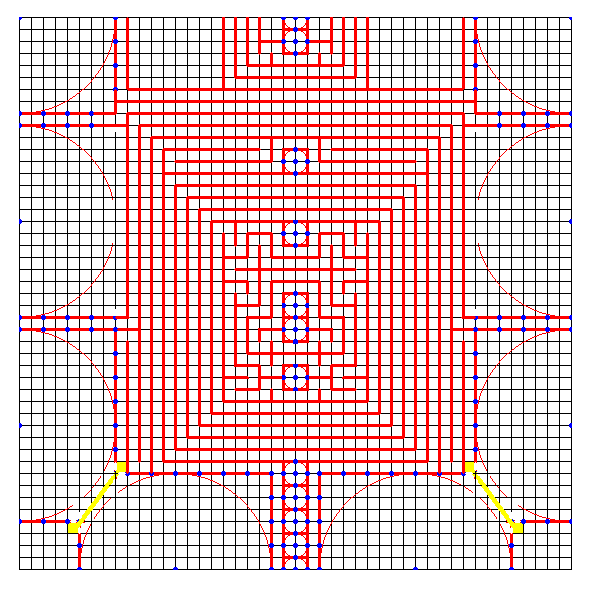
 蛇腹のカドは展開図上では方形領域として確保されることが多いが、方形以外のいろいろな形状を取れます。
蛇腹のカドは展開図上では方形領域として確保されることが多いが、方形以外のいろいろな形状を取れます。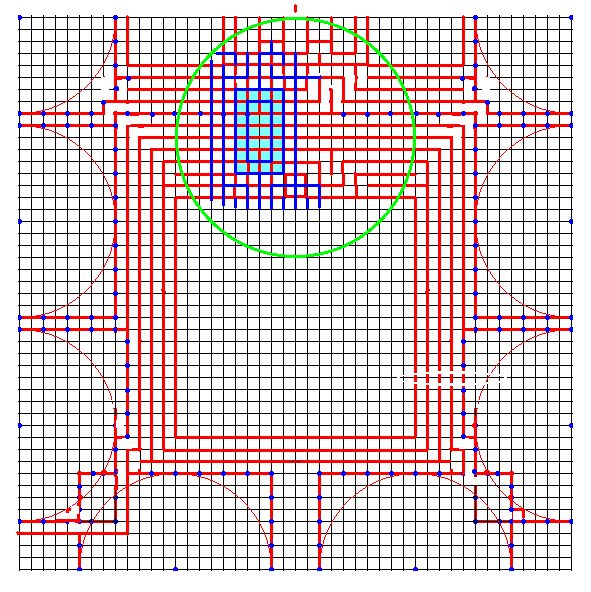

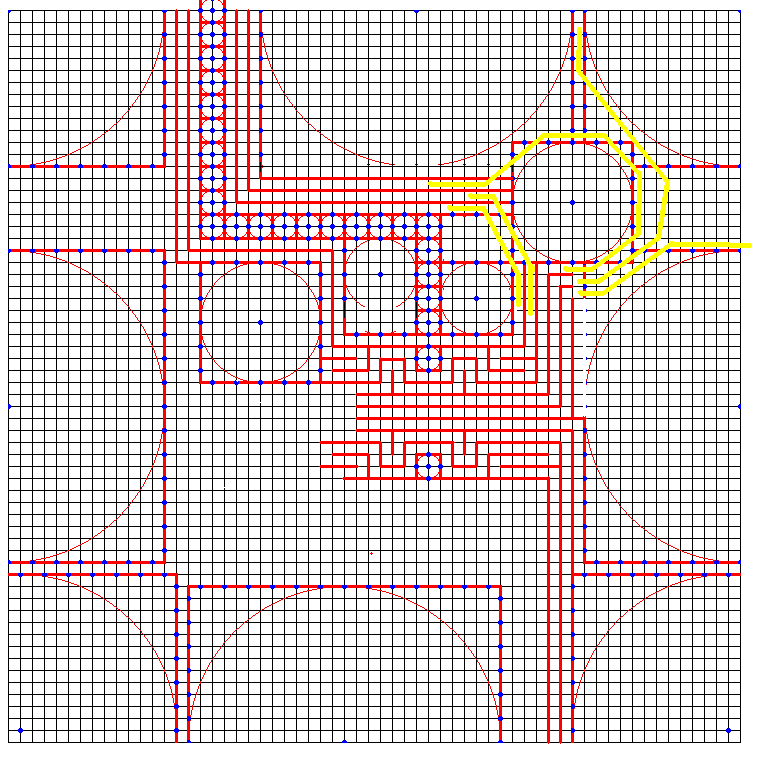
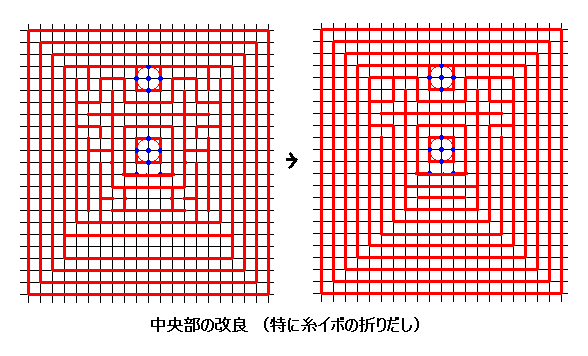
 [1220] の図の右側を再アップします。
[1220] の図の右側を再アップします。