「ずらし」パターンあれこれ
蛇腹の1/2ずらしから始まり、m/nずらし、無理数比ずらし。直角二等辺三角形の回転の幾何学
[1356] じゃばらじゃばらした折紙 投稿者:タト 投稿日:2003/07/23(Wed) 23:11
[1359] タトさん 投稿者:めぐろ 投稿日:2003/07/24(Thu) 20:03
[1362] パターン 投稿者:タト 投稿日:2003/07/24(Thu) 21:43
[1363] 誤差0 投稿者:めぐろ 投稿日:2003/07/25(Fri) 14:58
[1365] パイ(円周率)の公式 投稿者:めぐろ 投稿日:2003/07/25(Fri) 19:00
[1369] 1/2ずらし 投稿者:S太郎 投稿日:2003/07/27(Sun) 16:13
[1370] つづき 投稿者:S太郎 投稿日:2003/07/27(Sun) 17:55
[1371] 設計への応用 投稿者:タト 投稿日:2003/07/27(Sun) 18:06
[1372] という観点で見てたら 投稿者:タト 投稿日:2003/07/27(Sun) 18:22
[1373] 続き 投稿者:タト 投稿日:2003/07/27(Sun) 18:32
[1374] 無題 投稿者:S太郎 投稿日:2003/07/27(Sun) 19:48
[1377] 2分の1ずらし 投稿者:めぐろ 投稿日:2003/07/28(Mon) 19:52
[1378] 2分の1ずらし と帯領域のうねり 投稿者:めぐろ 投稿日:2003/07/28(Mon) 20:02
[1379] 新パターンの意義 投稿者:めぐろ 投稿日:2003/07/28(Mon) 20:14
[1380] n分の1ずらし 投稿者:めぐろ 投稿日:2003/07/28(Mon) 20:20
[1381] n分のmずらし 投稿者:めぐろ 投稿日:2003/07/29(Tue) 22:20
[1382] Re:[1381] n分のmずらし 投稿者:タト 投稿日:2003/07/30(Wed) 02:23
[1384] 無理数比のずらし 投稿者:めぐろ 投稿日:2003/07/30(Wed) 12:11
[1385] 1分の1ずらし 投稿者:めぐろ 投稿日:2003/07/30(Wed) 12:21
[1386] 3分の4ずらし 投稿者:めぐろ 投稿日:2003/07/30(Wed) 12:24
[1387] 1分の2ずらし 投稿者:めぐろ 投稿日:2003/07/30(Wed) 14:30
[1388] 3/2 投稿者:タト 投稿日:2003/07/30(Wed) 15:47
[1389] 面白いですね 投稿者:小松英夫 投稿日:2003/07/31(Thu) 01:50
[1390] 回転 投稿者:タト 投稿日:2003/07/31(Thu) 14:56
[1391] 原子の回転 投稿者:めぐろ 投稿日:2003/08/01(Fri) 20:17
BACK TO INDEX
ようこそ、折紙のホームページへ
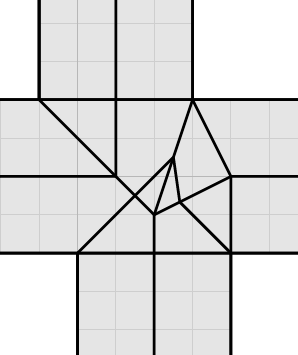 >微妙な誤差を含んでいるのでしょうか。
>微妙な誤差を含んでいるのでしょうか。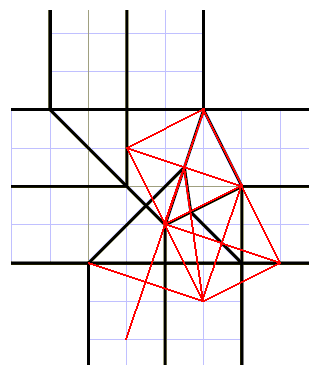 [1362] のタトさんの図をお借りして、適当に補助線を赤線で引いて見ました。
[1362] のタトさんの図をお借りして、適当に補助線を赤線で引いて見ました。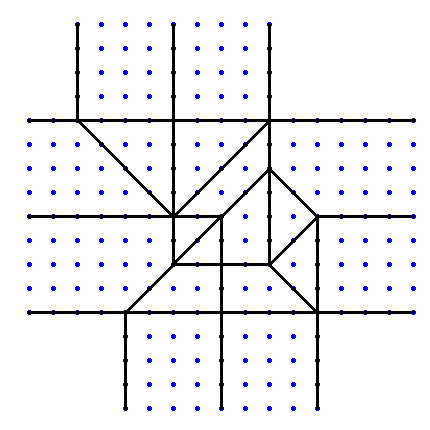 タトさんのパターンに比べればおもしろくありませんが、1/2ずらしについては、干渉部分内で1/2の蛇腹を使えば処理できるようです(図)。ただ、こうやって等高数とかを書き込めば内部で何がおこってるか把握しやすいかもしれません。(そう思うならやれって)
タトさんのパターンに比べればおもしろくありませんが、1/2ずらしについては、干渉部分内で1/2の蛇腹を使えば処理できるようです(図)。ただ、こうやって等高数とかを書き込めば内部で何がおこってるか把握しやすいかもしれません。(そう思うならやれって)
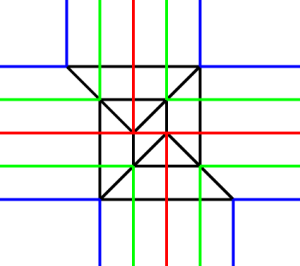
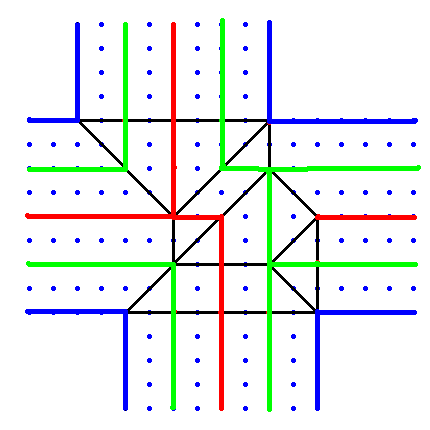 やってみました。赤が一番高いところ。緑が中間。青が低いところです。少しはみやすいかと思います。
やってみました。赤が一番高いところ。緑が中間。青が低いところです。少しはみやすいかと思います。
 実は非常にシンプルな形がありました。(なんで気づかなかったんだろう)
実は非常にシンプルな形がありました。(なんで気づかなかったんだろう)
 おそらくは真中の部分が二回反転しているので気づきにくかったのかもしれません。なんかやけに簡単になってしまった…
おそらくは真中の部分が二回反転しているので気づきにくかったのかもしれません。なんかやけに簡単になってしまった…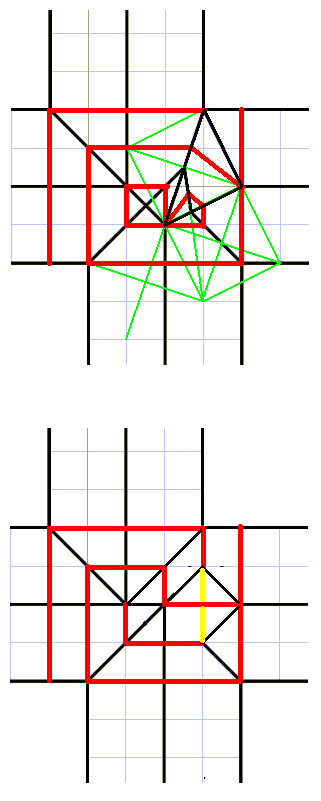 S太郎さんの[
S太郎さんの[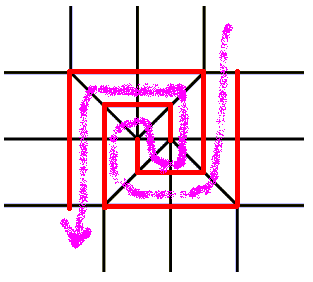 タトさんの[
タトさんの[ n分のmずらし の折り方は、タトさんの最初のパターンできれいに折れますね。うーん、これまた感動モノ。
n分のmずらし の折り方は、タトさんの最初のパターンできれいに折れますね。うーん、これまた感動モノ。
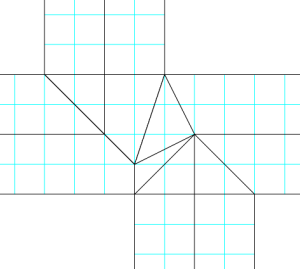 図は既にノートパソコンで使っていた3/2ずらしパターンです。
図は既にノートパソコンで使っていた3/2ずらしパターンです。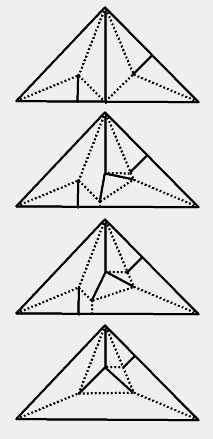 それぞれ折ってみながらいちいち納得しました。実際に折ってみないと紙の動きってなかなか読めないものですね。
それぞれ折ってみながらいちいち納得しました。実際に折ってみないと紙の動きってなかなか読めないものですね。
立体系蛇腹系の作品…というわけでノートパソコンを折っています。
図は一部分のパターンです。1/2ずらしパターンになっています。
このような1/2ずらしパターンと整数ずらしパターンを組み合わせたりしています。出来上がったら完全な展開図と写真を投稿させていただくつもりです…。なんとかコンベンションまでに作り上げたいと思っています。