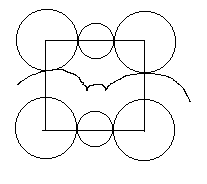円領域分子法といっても折紙設計をなされない方には何のことかわからないと思います。左図が円領域分子法の簡単な例です。
左図のような円と帯を用いた展開図の表示は、現在、世界中の折り紙関係のホームページで見られますので、円領域分子法という名前はしらなくても、左図のような円図を見たことがある人は多いと思います。
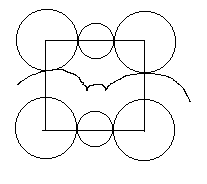円領域分子法といっても折紙設計をなされない方には何のことかわからないと思います。
円領域分子法が世界ではじめて発表されたのは、1991年10月5日発行の折紙探偵団新聞第十号です。この号の表紙ページに私が書いた実用折紙設計法NO.4という記事の中で、左図と以下の記載が掲載されています。
折紙探偵団新聞第十号の記事は簡単な原理を紹介したものですが、それより詳しい解説として、私が1994年6月25日発行の「をる No.5,p92-95」に書いた、折り紙解体新書第1回があります。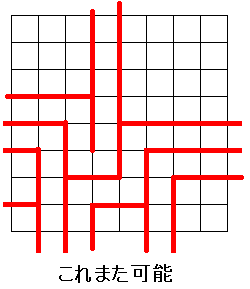
横分子蛇腹法についても、それがはじめて発表された状況について簡単にまとめてみたいと思います。
あまり、自分の作品について主張をしたいものではないのですが、ここ数年、円領域分子法の基本的原理を私以外の人も同時期に開発していたとか、私以外の人が開発したというような記事をしばしば目にするようになりました。
自分の開発した技法を多くの人に自由に使っていただくことが私の最大の目標の一つですが、自分の開発したことを他の人がやったこととして広められるのは、それはちょっと、、、と感じたりするわけです。
もし、折紙設計に関して不特定多数の人に公表する予定の方がこの掲示板を読んでおられましたら、これから円領域分子法ができるまでのいきさつについて簡単なまとめを書きますので、特に円領域分子法に関しては事実、特に円領域分子法に関する出版物の時期に即した書き方をしていただくようお願いします。
まあ、このようなローカル掲示板で書いても意味が無いような気はするわけですがいちおう主張だけはしておきたいと思います。