How to Divide the Side of Square Paper

Haga theorems

First, Haga first theorem is famous.

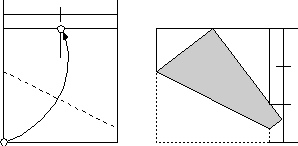
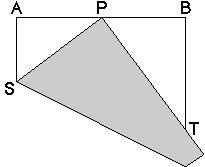
Let us verify it.

If the length of the side is 1, AP=BP=1/2. Let AS=x, and SP=1-x. Apply the Pythagorean theorem at triangle ASP and we get (1-x)²=x²+1/4, then x=3/8. Triangle ASP and triangle BPT are similar, and AP=BP=1/2, AS=3/8, therefore BT=2/3.

Second, there is Haga second theorem.

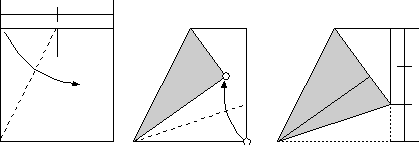
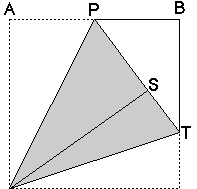
And here is the varification.

If the length of the side is 1, PB=PS=1/2. Let BT=x, and ST=1-x. Apply the Pythagorean theorem at triangle PTB and we get (1/2+1-x)²=x²+1/4, then x=2/3. Therefore BT=2/3.

The third one is, of course, Haga third theorem.

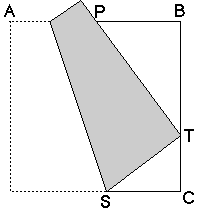
The varification is rather complex.

If the length of the side is 1, PB=1/2. Let BT=x, and TC=1-x. Since triangle PBT and triangle TCS are similar, CS=2x(1-x). Therefore ST=1-2x(1-x). Apply the Pythagorean theorem at triangle TCS and we get (1-2x(1-x))²=(1-x)²+(2x(1-x))². We have two solutions: x=0 or x=2/3. Since BT is not 0, BT=2/3.