How to Divide the Side of Square Paper

More trisection

This way is also well known. Here we divide the diagonal, so we divide the width and the height at the same time.

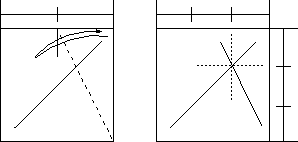
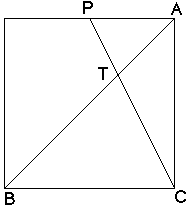
The verification is easy.

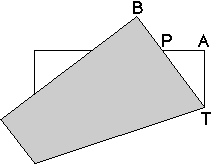
Triangle APT and triangle BCT are similar, and BC=2AP, then BT=2AT. Therefore AT=AB/3.

This way was presented by KAWAHATA Fumiaki in Origami Tanteidan Newsletter issue 29.

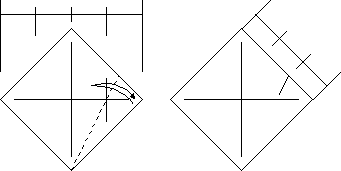
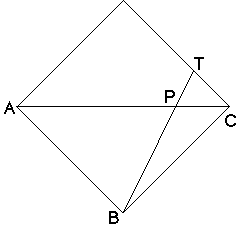
The verification is easy, too.

Triangle ABP and Triangle CTP are similar, and CP=AP/3, therefore CT=AB/3.

The next way was presented by NOMA Masamichi in Origami Tanteidan Newsletter issue 14. The advantage of this method is to keep the center part of paper unfolded.

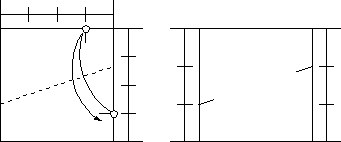
Let us verify this.

If the length of the side is 1, AP=BP=1/4. Let AT=x, and PT=3/4-x. Apply the Pythagorean theorem at triangle APT and we get (1/4)²+x²=(3/4-x)², then x=1/3.