How to Divide the Side of Square Paper

Yet another, and pentasection

FUSE Tomoko showed this way in her book "Unit Origami" (1983). We also trisect the right angle here.

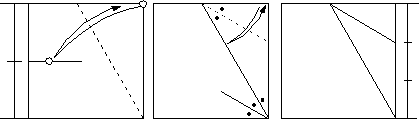
Here is the valification.

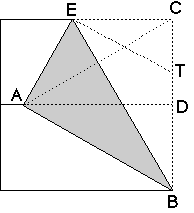
Because AB=BC and AB=AC, triangle ABC is equilateral. So the angle ABC is 60 degrees. Angle ABE=angle CBE, then angle CBE is 30 degrees, and angle CEB 60 degrees. So BE:EC=2:1. Angle BET=angle CET, and BT:TC=BE:EC=2:1.

How about dividing into 5? Actually, you have already done before.

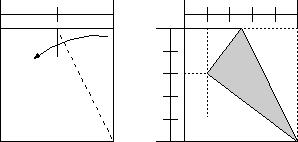
The verification is complex.

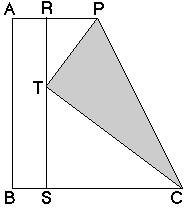
Let the length of the side 1 and AR=BS=x, then PR=1/2-x, SC=1-x. Triangle RTP and triangle SCT are similar, and TC=2PT, then RT=SC/2=(1-x)/2, TS=2PR=1-2x. Because RT=1-TS, RT=2x. Therefore (1-x)/2=2x, then x=1/5.