折り紙の辺を等分する法

芳賀定理

まずは、有名な芳賀第一定理。

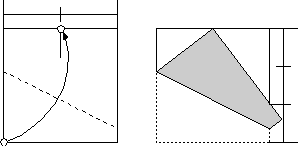
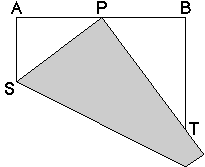
計算で確かめてみましょう。数学に自信のない方は読み飛ばしても結構です。

辺の長さを1とすれば、AP=BP=1/2です。また、AS=xとするとSP=1-xです。三角形ASPに三平方の定理を適用して、(1-x)²=x²+1/4より、x=3/8が得られます。 三角形ASPと三角形BPTが相似で、AP=BP=1/2,AS=3/8より、BT=2/3となります。

次に、芳賀第二定理。

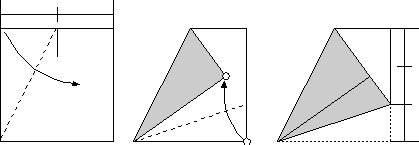
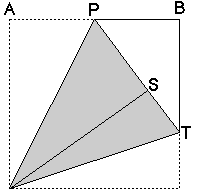
これも証明してみます。

辺の長さを1とすれば、PB=PS=1/2です。BT=xとすると、ST=1-xになります。三角形PTBにピタゴラスの定理を適用して、(1/2+1-x)²=x²+1/4より、x=2/3が得られます。したがって、BT=2/3です。

三番目は、もちろん、芳賀第三定理です。

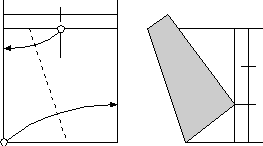
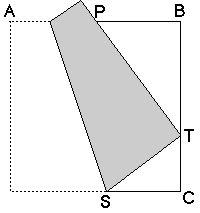
証明はちょっと面倒です。

辺の長さを1とすれば、PB=1/2です。BT=xとすると、TC=1-xです。三角形PBTと三角形TCSが相似ですから、CS=2x(1-x)で、ST=1-2x(1-x)となります。三角形TCSにピタゴラスの定理を適用すると、(1-2x(1-x))²=(1-x)²+(2x(1-x))²となります。この方程式の解は2つあって、x=0またはx=2/3ですが、BTは0ではないので、BT=2/3となります。