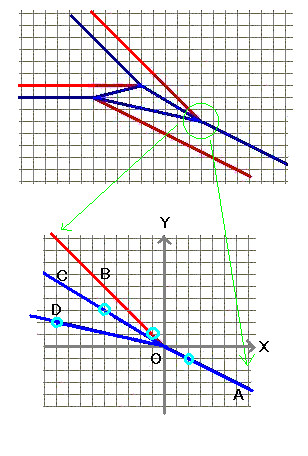左図の上図は、ある、ねじり折りのパターン左図の下図は、上図のねじり折りの頂点の一つを拡大して、座標軸をつけたものです。
ここで、以下のことに注目してください。
折線Ａは座標（2,-1）を通ります。そこを水色の円で印をつけておきました。
折線Ｂは座標（-1,-1）を通ります。そこも水色の円で印をつけておきました。
折線Ｃは座標（-5,3）を通ります。そこも水色の円で印をつけておきました。
折線Ｄは座標（-9,2）を通ります。そこも水色の円で印をつけておきました。
このように、方眼格子の上でねじり折りなどをすると、その折線が予定調和的にあちこちの格子点の真上を通過するという現象が起こります。
ここで、方眼格子点の任意の異なる２格子点の上を通る折線を格子点上折線ということにすると、「格子点上折線のみで構成される展開図でも予定調和的整合性が出てくる」わけです。
なぜ、このような予定調和性がでてくるかを考えてみましょう。
具体的な例として、左下図で、最初に格子点上折線の条件を満たすようにして折線A,B,Cを決めたとしましょう。
そこにから頂点Oが平面に折りたためるように折線Dを発生させた場合、折線Dもまた格子点上折線になることを見てみましょう。
例えば、左下図の折線Aの傾きは -1／2 ですが、このときx軸と折線Aのなす角度は、tanの逆関数をatnとして、atn（-1／2）となります。
一般に頂点Oを通る折線がO以外の格子点の上を通るということは、その折線の傾きが
atn（I／J） I,Jは任意の整数
という形で表せるということと同じです。
この形で表せる角度を集めて、集合Kとしておきましょう。
（というか、この定義だとJが０のとき困ってしまうのだが、まあ、大まかな流れということで,,,）
すると、以下のことがわかります。（s ∈ K はｓはKに含まれるという意味）
s ∈ K かつ t ∈ K ならば、s+t ∈ K
同様に
s ∈ K かつ t ∈ K ならば、s-t ∈ K
なぜこうなるかは、後でかきます。
具体的にいうと、左下図で、頂点Oから出る折線A,B,Cは、それぞれ、対応する格子点の上を通るので、その折線の傾きは、
atn（I／J） I,Jは任意の整数
という形で表せます。
したがって、各折線A,B,Cとｘ軸がなす角度をそれぞれa,b,cとすると、
a∈K, b∈K, c∈K です。
ここで、頂点Oが平面に折りたためるように折線Dを発生させ、折線Dとｘ軸がなす角度をdとしましょう。
ｄ＝c＋角度COD
ですね。
このとき、角度COD は 180度‐角度AOBですから
ｄ＝c＋180度‐角度AOB
ここで、角度AOB = b-a ですから、
c＋180度‐(b-a)＝180度+a‐b+c
です。
180度∈K、a∈K, b∈K, c∈K ですから、
ｄ∈Kです。
したがって、d は
atn（I／J） I,Jは整数
と表せるので、折線Dは座標（I,J）の格子点上を通ります。
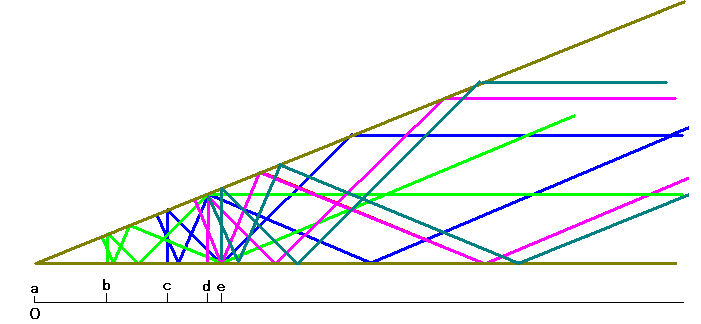
ご無沙汰してます。復帰されてからいつも覗かせていただいてますが、書き込む機会を逸してしまってましてすみません（汗）。面配置法・蛇腹顔などなど、どのトピックも刺激的です。
22.5度系のメッシュの縮重のようすを評価するため、まず、平面の上に1点を置きます。
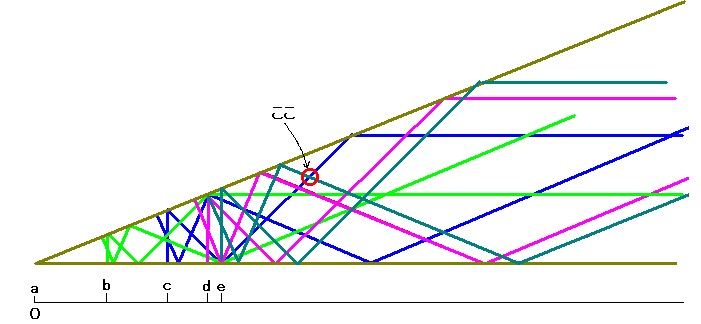
22.5°系で2点A,Bが与えられたときに新たに発生しうる頂点を図に描いてみました。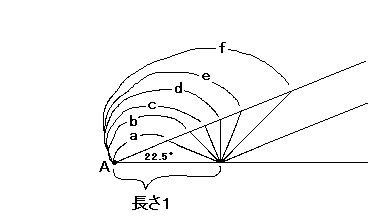
左図で、22.5°系において、長さ１の折線を22.5°回転すると、可能な折線の長さは、a か b か c か d か e か f のいずれかしかありません。22.5°回転の操作を16回やると、22.5×16＝360でちょうど頂点Aの周りに一回りしたことになります。
[2097]の考え方はかなり有力な気がします。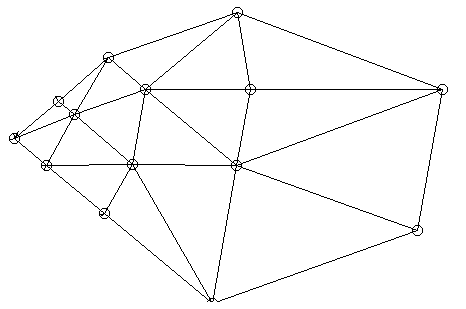
20度系でとりあえず折線をつけてみました。
例えば、22.5度系なら、その展開図にある折線のなす角は全て、22.5度の整数倍になっています。
このような折線構成がうまくいくのは、折線の交叉する頂点において、頂点周りの角度を順に+、-、+、-と加えていった合計が０度になるという条件（これは、折線の交叉する頂点が平面的に折れるための必要条件）が、予定調和的に満たされやすいから、というのが、一つの考え方としてあります。
すごく大雑把な話をすれば、このような予定調和的性格は、22.5度系や15度系の角度系に限ったことではなく、180度の整数分割系の角度系ならみな持っています。
たとえば、20度系の折線構成でも22.5度系や15度系と似た予定調和が起きます。ただ、20度という角度を折るのは、22.5度や15度のように自然に折れるわけではないという問題はありますが、、、、、
10度系でも36度系でも予定調和的整合性は出てくるのですが、だからといって、2度系とか、1度系にしてしまうと、角度パターンが多すぎて、予定調和的整合性の恩恵を受ける確率が少なくなってしまいます。
例えば、22.5度系なら、可能な角度は、
22.5度, 45度, 67,5度, 90度, 112.5度, 135度, 157.5度
の７通りしかありませんが（180度以上の角度は平面に折りたためる展開図上には存在しない）、
15度系なら、可能な角度は、
15度, 30度, 45度, 60度, 75度, 90度, 105度, 120度, 135度, 150度, 165度
の11通りあるわけです。
10度系なら、可能な角度は、
10度, 20度, 30度,,,,,150度, 160度, 170度
の17通りあるわけです。
これが1度系になってくると、展開図上の折線のなす可能な角度は、
1度, 2度, 3度,,,,,176度, 178度, 179度
と179通りにもなります。
これでは、22.5度系のように、折っていてぴたっと折線が重なるというような偶然がたやすく起こるわけがありません。
こんなわけで、予定調和を引きおこす角度系は、22.5度系でも、20度系でも、15度系でも、10度系でも、36度系でも、2度系でも、1度系でも、90度系でも、45度系でも、なんでもいいのですが、その予定調和的気持ちの良い折り方が実現する確率を上げるためには展開図上に現れうる角度パターンの数はある程度少ない方がいいのです。
ただ、現れうる角度の数が少ない方がいいからといって、90度系とかを使うと、これは、展開図上の折線のなす可能な角度パターンは、
90度
のただ1通りですから、折線が単純で、折っていて折線が重なるというようなことは、奇跡的な偶然ではなく、あたりまえのこととして感じられます。これでは予定調和的快感はなくなってしまいます。
45度系（これは蛇腹の折線系）ではどうでしょうか。45度系展開図上の折線のなす可能な角度は、
45度, 90度, 135度
の３通りです。90度系よりはずっと複雑ですが、まだ、予定調和的快感を感じるには、現れうる角度が少なすぎて、蛇腹で、予定調和的快感を感じるという人はあまりいないでしょう。
30度系ではどうでしょうか。30度系展開図上の折線のなす可能な角度は、
30度, 60度, 90度, 120度, 150度
の５通りで、この辺から予定調和的快感を感じる人も、多少いるのではという気がします。
以上のようなことを考えると、予定調和的整合性を快く感じることができる角度系は10度系か30度系の間にあるのではと個人的には思います。その中でも、折りやすさを考えれば、22.5度系が最も有利で、15度系がそれに続きます。これ以外の角度系としては、折紙設計的な興味から、20度系が魅力的ですが、多分まだ作例はないと思います。
以上は整数の角度を生成元にする角度系での予定調和ですが、それらとはまた違った角度系でも予定調和的整合性は出てきます。（以下続きます）