第4章 作品批評
『あざらし』『リス』『桜』
(折紙探偵団新聞第50・52・54号)
これまで、個々の作品について云々という話を二度ほどいったと思います。二度あることは三度ある、とならないためにも、公約を実行しようと思います。
笠原邦彦『あざらし』
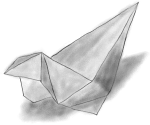 図1
図1
最初に取りあげるのは、笠原邦彦の作品です。まず、図1をご覧ください。何にみえますか。あざらしにしかみえませんよね。そう、『あざらし』です。最初はあざらしにみえなかった人も、あざらしだと聞けばあざらしにみえるのではないでしょうか。そして、いったんあざらしにみえたが最後、あざらし以外のものにはみえなくなります。前章で紹介した象もそうですが、これこそ具象の局地。抽象こそ究極の具象なのですね。
さて、このことを「見立て」という観点から考えてみましょう。それも、作品を創作する立場ではなく、作品を眺める立場から考えてみます。
そんなものがあるかどうか知りませんが、『リアルなあざらし』という作品があったとします。専門家にみせたら「おお、これはバイカルアザラシだね」などといわれるかもしれません。そのような作品があざらしにしかみえないのはごく当たり前のことです。それは見立てるまでもなく、あざらしにみえてしまいます。リアルな作品は、何かに見立てるということができないといってもよいでしょう。
それに対して、笠原の『あざらし』は、あざらしにしかみえないにもかかわらず、なぜあざらしにみえるのか不思議です。なぜ不思議なのかといえば、この作品が作品として、実物のあざらしとは独立に存立しているからではないでしょうか。つまり、この作品はあざらしでなくてもよかったのに、あざらしにみえるから、不思議に思えるのです。もし地球上にあざらしなる生き物がいなかったとしても、この作品は存在するでしょう。もちろん、その場合は、あざらしではない、別なものに見立てられるでしょう。
折り紙を観賞するとき、鑑賞者は「折られた紙」を見ることになります。内山光弘は「折り数が増えることによって、せっかくの美しい紙がどんどん死蔵されてしまう」といったそうですが、このことは、特に複雑な作品の場合、省みられない傾向があります。確かに、紙をざっくりとみせるということはとても勇気のいることです。ですが、よけいな折りをそぎ落として、紙に語らせることによって、折り紙作品が彫刻作品に比すべき存在感をもつことができるのです。
そういう意味でいえば、この作品も「絶対折り紙」としての要素をもっているといえます。私の考えでは、名作はすべからく絶対折り紙でなければなりません。『リアルなあざらし』が、実物のあざらしと似ているということだけでしか評価できないとしたら、いいかえれば、「折り」は評価できるが「紙」は評価できないとしたら、すぐれた折り紙作品であるとはいえません。
「絶対折り紙」・「標題折り紙」という概念は、論理学でいう内包的性格をもっていると考えられます。折り紙作品を、この作品は絶対折り紙、この作品は標題折り紙、というように、二つの集合に分けることはできません。ある一つの作品が、見方によって、絶対折り紙になったり、標題折り紙になったりします。
さて、この作品は標題折り紙としての要素ももっていて、その点で以前紹介したジャクソンの一線折りとは異なっています。最後に、このことについて考えてみましょう。
ジャクソンの一線折りは、何かに見立てられているわけではないのに、名作たり得ます。それは、「紙」そのものが、美しかったり、優しかったり、官能的だったりするからです。この場合、「紙」と「かたち」が直結しています。
では、『あざらし』はどうでしょうか。『あざらし』を、あざらしとしてみずに、「そのようなかたちをした紙」としてみたとすれば、正直にいって、たいしておもしろいかたちではないと思います。もしもこの作品が何にも見立てられなかったとしたら、あるいは見立てがうまくいかなかったとしたら、この作品は決して名作にはならなかったでしょう。
ここに見立てのおもしろさがあります。それ自体はなんということもないものが、何かに見立てられたとたん、様相が一変するのです。今まではただの紙にすぎなかったものが、生命を得て躍動しはじめます。この歓びこそ、スーパーコンプレックスでは味わえない、「初級」作品の醍醐味です。
小松英夫『リス』
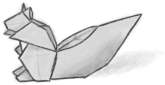 図2
図2
次に取りあげるのは、小松英夫の『リス』です。この作品の最大の魅力は、太い尻尾にあると思います。では、この尻尾がどのように折り出されているか、構造図で見てみましょう。(図3)
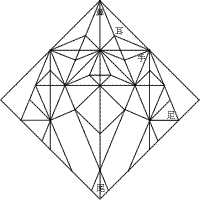 図3
図3
構造図を見ると、作品全体は22.5度ないしその倍数の角度で交わる折り線によって構成されています。このような作品は、すべての折り線が有機的に関連し合っているという点に特徴があります。そのとき、展開図そのものが美しいものになりますが、それだけでなく、折っているときにも、カドとカド、辺と辺がピタリピタリと合って、心地よい感触を覚えます。
しかし、この作品のよさはそれだけではありません。図でいうと上の方、リスの頭や手の部分は典型的な構造を示していますが、足と尾の部分はちょっとおもしろい構造になっています。
ふつう、尻尾などのカドを折り出す場合、正方形の頂点から22.5度の線がでるようなかたちにします。しかし、この作品では、上の方からやってきた2本の22.5度の線は、頂点の手前で交わってしまいます。そのことによって、尻尾に使える領域が大きくなり、太い尻尾を折り出すことが可能になっているのです。
通常の設計法では、尻尾の長さだけが問題になりますので、このような発想はなかなか生まれません。これは私の勝手な想像ですが、小松も、このような効果を期待して設計をしたのではないのではないでしょうか。
問題の22.5度の線を上にたどってゆくと、これらの線は、もとの正方形の辺を2等分する点からでていることがわかります。一方、正方形の上の頂点から出発した22.5度の線は、正方形の下側の辺にぶつかり、これらの辺を1対ルート2に分割します。
通常、22.5度の折り線で構成された作品では、1対ルート2の分割が基本になります。そうすることで、すべての分子が正方形の中に隙間なく埋め込まれるのです。しかし、この作品では、1対ルート2の分割と、それとはまったく異質な1対1の分割が、一つの正方形の中に共存しているのです。
そのことによる効果として、図4で網掛けで示した部分が小さな正方形の外側につけ加わったようになり、この部分が太い尾を可能にしているのです。
 図4
図4
さて、ここで強調したいことは、この網掛け部分の正方形全体に対する割合が、この作品の尾をつくるのにちょうどいい割合になっているということです。この部分がもう少し長くても、もう少し短くても、この作品はバランスを失ってしまうでしょう。
この割合は、1対1と1対ルート2という、折り紙におけるもっとも基本的な2種類の分割を一つの正方形に共存させたことから生じさせたのでした。その結果として生じた網掛け部分の幅がリスの尾にちょうどよい幅であるということは、小松がこの効果を意図的にねらっていたのだとしても、僥倖というべきでしょう。
私が思うに、すべからく名作は、このような僥倖に恵まれています。もちろん、僥倖を逃さず、作品のかたちに結実させるのは、創作者の能力にほかなりません。しかし、どんなにすぐれた創作者でも、僥倖がやってこなければ、名作を生むことはできないのではないでしょうか。
これは、折り紙が制約を伴う芸術であるということと関係しています。もちろん、どんな芸術にもなんらかの制約はあります。例えば音楽にしても、ピアニストの指は10本しかありませんし、バイオリンの弦は4本しかありません。でも、これらの制約は、折り紙における不切正方一枚という制約とは比べものになりません。
設計法の発達によって、とりあえずかたちをつくるためだけなら、不切正方一枚は制約ではなくなりました。しかし、名作をつくろうと思ったら、あいかわらず不切正方一枚は制約であり続けています。
このような制約のもとで創作をするとき、創作者は、創造神の如くふるまうことはできません。折り紙では、あくまで紙が神なのであって、紙の神の微笑みを受けた作品だけが名作となりうるのです。
川村みゆき『桜』
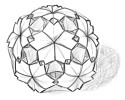 図5
図5
最後に、川村みゆきの『桜』を取り上げます。この作品を見るまで、ユニット折り紙は、折り紙としてはとるに足らないものだと思い込んでいました。この作品は、その蒙を啓いてくれました。
私がユニット折り紙に折り紙としての魅力を感じなかったのには理由があります。
まず、同一のユニットを何十枚、何百枚と使って動物などをつくることがありますが、これが折り紙としてはおもしろくありません。ユニット折り紙で動物をつくったとき、造形の手段として主に使われているのが、紙を折ることではなく、紙を組むことであるからです。これがおもしろいとしても、それはユニットを組み立てるおもしろさであって、折り紙のおもしろさではありません。
ユニット折り紙で立方体などの幾何学的な立体をつくることがありますが、これもまた折り紙としてはおもしろくありません。このことは、ユニット折り紙に限らず、一枚折りの作品にもいえることです。正方形の紙から立方体を折るのは、実際おもしろいことですが、そのおもしろさは、数学的なおもしろさ、あるいはパズルとしてのおもしろさです。パズルは解いているあいだが楽しいのであって、解けてしまうと、もう一度解きたいと思うのではなく、次の問題を解きたいと思うのです。これは折り紙のおもしろさではありません。優れた作品を折ると、もう一度この作品を折りたいと感じます。折り手に何度でも折りたいと思わせる作品でなければ、名作とはいえません。
また、幾何学的な作品は、折っているときは楽しめますが、折り上がってしまえばそれで終わりです。立方体を眺めていても、おもしろくもなんともありません。折り紙は折り手だけのものではありません。紙を折らない人でも、作品を作っているところを見たり、作品そのものを見たり、あるいは作品で遊んだりして、楽しめなければなりません。演奏するのは楽しいけれど聞いてもつまらない音楽作品が名曲とはいえないのと同じように、折った後でも楽しめる作品でなければ名作とはいえません。
私が思うに、折り紙のおもしろさは、無機的な、単純な形をした紙から、有機的な、生き生きとした形が生まれるところにあります。以前、カブトムシの形をした紙からカブトムシを折ってもおもしろくないといいましたが、それと同じように、正方形の紙から正方形を折ってもおもしろくありません。
おそらく、ユニット折り紙の真価が発揮されるものの一つはくす玉だといえるでしょう。くす玉のポイントは表面の凹凸にあります。多くのくす玉は幾何学的な立体をもとにしていますが、表面の凹凸があるおかげで、有機的な、見る人に何かを語りかけるような形になっているのです。
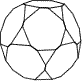 図6
図6
正十二面体のそれぞれの頂点を切り落とすと、三角形20個と十角形12個からなる立体ができます(図6)。『桜』はこの立体をもとにしています。しかし、この立体自体は見ていてもおもしろいものではありません。『桜』は、この幾何学的な立体からずれていて、このずれが表現力を持っているのです。たとえば、360度を5等分すると72度ですが、『桜』の花びらの中心角は72度より小さくなっています。(計算すると、およそ70.5度になります。)そのため、組んだときに、花が平面にならず、中心が少しへこみます。そのことによって、花の立体的な表現が可能になっているのです。
さらに、この作品の優れたところは、花びらの表現にあります。花びらの形は、折り目によって表現されています。つまり、紙を折ることが表現の手段として使われています。その意味で、ちゃんと折り紙になっています。しかし、この作品は同時にユニット折り紙であり、紙を組むこともまた表現の手段になっています。ユニットを組んでゆくと、それぞれのユニットが引っ張り合い、個々のユニットが適切な角度で自然に曲げられます。そのため、使われている折り目がすべて直線なのにもかかわらず、この作品はむしろ丸みを感じさせます。そして、この曲がり具合が花びらの表現に大きな役割を果たしているのです。
ユニット折り紙は、紙を折って組むわけですから、その表現において、折ることと組むことがバランスよく組み合わされていなければなりません。この作品は、紙を折ることと紙を組むことの表現力を、高いレベルでバランスよく発揮した作品として、特筆するべきだと思います。
![[home]](../../../global/ToHome.gif)
![[第3章]](../../../global/Left.gif)
![[back]](../../../global/Up.gif)
![[第5章]](../../../global/Right.gif)