折り紙の辺を等分する法

三等分をもう一つ、さらに五等分

布施知子著『ユニット折り紙』（1983）に、次の方法が紹介されています。この方法は、30度・60度の角度を折り出す方法も示しています。

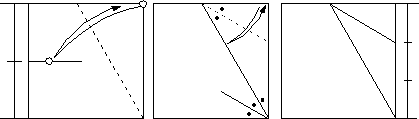
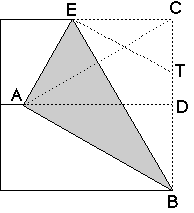
証明は次の通りです。

三角形ABCについて、AB=BCです。また、ADはBCの垂直二等分線ですから、AB=ACです。したがって、三角形ABCは正三角形で、角ABC=60度です。角ABE=角CBEより、角CBE=30度。よって角CEB=60度となります。したがって、BE:EC=2:1です。角BET=角CETより、BT:TC=BE:EC=2:1です。

さて、5等分はどうでしょうか。実は、あなたはすでに5等分をしたことがあります。

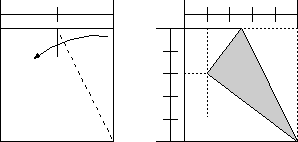
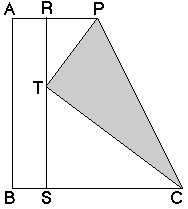
計算はちょっとめんどうです。

辺の長さを1として、AR=BS=xとします。すると、PR=1/2-x、SC=1-xです。三角形RTPと三角形SCTが相似形で、TC=2PTですから、RT=SC/2=(1-x)/2、TS=2PR=1-2xです。 一方、RT=1-TSより、RT=2xとなります。したがって、(1-x)/2=2xという方程式が得られ、x=1/5となります。