会場

筑波大学筑波キャンパス（天王台キャンパス） 総合研究棟B棟 1階 110室

つくば駅より筑波大学循環バス（右回り）乗車（約15分）、第一エリア前下車

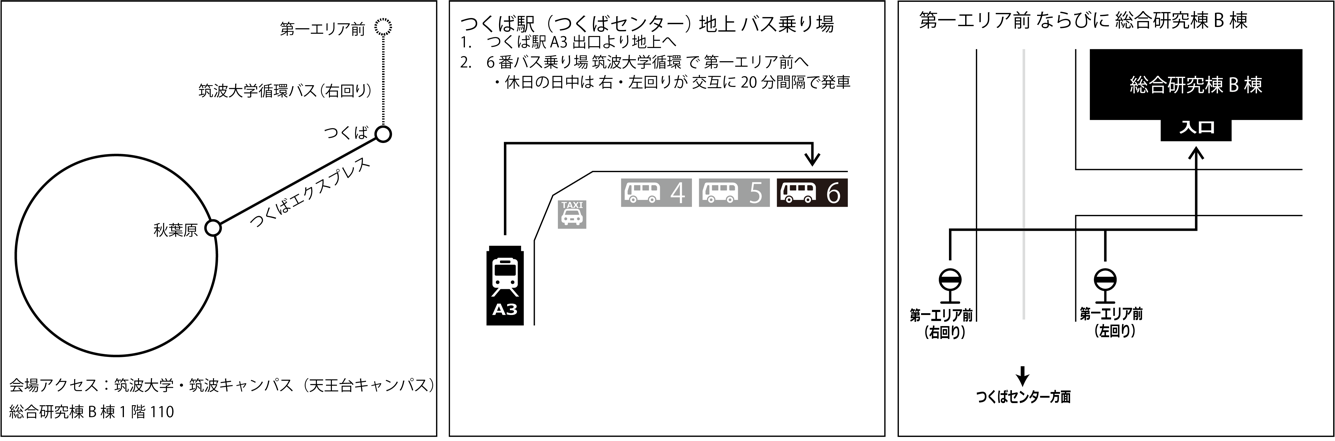
筑波大学アクセス　会場付近の地図　つくば駅バスターミナルマップ　バス時刻表

日程・概要

• 5月18日（土）
  • 13:30-14:40 : ワークショップ（現地参加者のみ）
  • 15:00-15:40 : 短時間口述発表（オンライン配信あり）
  • 15:40-16:20 : フリートーク
  • 16:20-17:00 : 三谷研究室見学（現地参加者のみ）
  • 19:00-21:00 : 懇親会（つくば駅前の飲食店を予定）
• 5月19日（日）（オンライン配信あり）
  • 10:00-11:50 : 口述発表
  • 11:50-13:00 : 昼休み
  • 13:00-17:00 : 口述発表

---

懇親会

• 時刻：5月18日（土）19:00- 21:00
• 会場：北海道魚鮮水産 BiViつくば店（つくば駅前）
• 参加希望者は、参加申し込み時にチェックをいれてください（5/16までにお願いします）。
• 料金は、約5000円を当日申し受けます。

---

弁当（5/19）

• 休日は学食が営業していません。近郊にはレストランがあまりありません。
• 弁当を希望するかたは、参加申し込み時にチェックをいれてください（5/17までにお願いします）。
• 次の2種類の予定です。1100円程度（京風折箱弁当）、800円程度（和風唐揚げ弁当）
• 料金は、当日申し受けます。

---

参加費

• 一般参加（現地）：2000円
• オンライン参加：1000円
• オンライングループ参加（ひとつの端末を複数人で視聴）：2000円

---

申し込み

事前に申し込みをしてください。

---

プログラム

2024年5月18日（土）

オンライン配信（予定）：15:00-16:00

13:30-13:40	おしらせなど
13:40-14:10	ワークショップ：曲線で折る折り紙「球体8枚羽根」と「タマゴのラッピング」　三谷純 曲線での折りを含む「球体8枚羽根」と「タマゴのラッピング」の2作品を制作します。あらかじめ折り筋が加工された型紙を配布します。
14:10-14:40	ワークショップ：折り線つきの紙で「骨格のある正八面体」をつくる　前川淳 6枚組の作品「骨格のある正八面体」を、折り目が印刷された紙によって製作する。本作品は複数パーツを組み合わせるユニット折り紙である。用意された紙により個々のパーツはきわめて簡単にできるが、それらの組み合わせは、慣れないひとにはすこし手強いパズルとなるだろう。作品は、正八面体という立体の構造の把握させるものとして教育的でもある。
14:40-15:00	休憩、および、オンライン接続準備
15:00-15:10	短時間発表：ピローボックスの容積を最大化する折り目曲線の考察　三谷純 過去にもピローボックスの容積を最大化する折り目曲線に関する考察を紹介したが、その際は曲線をベジェ曲線で表現し、制御点の位置を最適化するものだった。今回、折り目曲線の半分を1000の区分に分け、区分線形補間による折り目曲線表現を行うことで最大値の算出を行ったので、その結果を報告する。
15:10-15:20	短時間発表：紙テープが作る螺旋に対する数学的考察　三谷純、三浦憲二郎、R.U. Gobithaasan、Md Yushalify Misro 書籍「SPIRAL-ORIGAMI|ART|DESIGN（Tomoko Fuse）」(p51)に紹介されている、SPIRAL FROM TAPEが作る頂点の配列がSpiral of Theodorusの頂点列に対応することが知られている。紙テープの幅を1としたときに、この螺旋は幅が1の常螺旋に近づくことと、紙テープの幅が一定でないとした場合、点列を常螺旋上に乗せることができることを示す。
15:20-15:30	短時間発表：3Dプリンタによる双安定ユニットの制作　Pamela Higa、三谷 純 3Dプリンタによる大型構造物の造形には限界があるという問題を解決するために、平らに折りたたまれた状態を出力し、そののちに展開できる構造を作成するシステムを提案する。これにより、印刷時間を短縮し、サポート材料の廃棄を抑え、3Dファブリケーションの機能を拡張することを目指す。本研究では、双安定な折り紙構造を対象とし、折り目にダブルヒンジを組み込み、高精細アクリルで出力を行った。
15:30-15:40	短時間発表：折紙ベースの建築アプローチとしてのハフマンの楕円の再現　Aida Safary、三谷純 本研究はRhino+Grasshopperをモデリングツールとして、David Huffmanによる2頂点の楕円の曲線折り紙デザインを再現することを目的とする。その意図は、様々なデザイン要素における建築コンセプトとしての応用を探ることにある。ユーザは楕円デザインのパラメータと制約を操作することができ、それによりインタラクティブな方法で、折りの動作とモデルの3次元構造に関する洞察を得ることができる。
15:40-16:20	フリートーク 参加者による、簡単な自己紹介と最近興味があることなどについて。
16:20-17:00	三谷研究室見学

2024年5月19日（日）

オンライン配信

10:00-10:05	おしらせなど
10:05-10:25	折り紙によるダブル・キュービック・コアの実現と応用　谷口智子、上原隆平 キュービック・コアとは、1枚の紙に等間隔に正方形の穴を開けて折って作る構造であり、上下の面が凸凹の市松模様になる特徴がある。2枚のキュービック・コアをずらして重ねれば、全ての面の高さを揃えられる。これをダブル・キュービック・コアと名付ける。本研究ではまず，ダブル・キュービック・コアの構成方法を提案する。また応用として表裏でドットパターンを出す方法と、それに基づいてデザインしたフォントを紹介する。
10:25-10:45	切紙式立体空間構造　宮本好信 回転建立方式(RES)の単元を連続連結して塔状、板状の立体構造を作る方法(RES Space Frame)を紹介する。FDM方式3Dプリント試作による製作実証とFEMのよる実用検討を説明する。
10:45-11:00	平坦折り紙のHetying代数構造　賈伊陽 平坦折り紙の各折り畳み状態は面の重なり順によって一意に決まる。平坦状態の全体が形成する集合には、自然に定義される半順序が存在し、圏構造を定義することができる。この圏はデカルト圏であると証明可能である。さらに、平坦状態に対するヘティング代数構造を構築することができる。
11:00-11:05	休憩
11:05-11:20	大星型12面体の表面の連続的平坦折りたたみと翼折り　奈良知惠 星型正多面体は4種類で，その一つである大星型12面体は正20面体の各面に高い正三角錐の突起を付加した形状である。この表面を切ったり伸縮させたりせずに自己交差なく連続的に平坦に折りたたむ問題について考える。この突起を単独に取り外して平坦化することは容易であるが，20個の三角錐を接着した状態で平坦化するには互いの衝突を回避する工夫が必要である。そこで，翼折りを複合的に適用して実現できることを示す。
11:20-11:35	直線状エアパウチで実装された剛ルーリング曲線折紙　張一葦、舘知宏 曲線折紙は曲線に沿ってシートを折る折紙で、ルーリングが剛であると仮定すると一自由度メカニズムを構成できます。本研究では、剛ルーリング曲線折紙を軽量素材で実現する方法として、エアパウチをルーリングに沿って配置し、折り目で分節する構造を作ります。理論モデルと物理モデルの比較実験を通じて、提案手法の有効性を示します。
11:35-11:50	一定の角度をなして開いた二つ折りの紙の間の折り紙押出成形　土井 護 ポップアップカードや茶谷による折り紙建築は、切り込みを入れた二つ折りの紙を一定角度で開いたときに立体が現れるしくみである。本発表では、このように一定角度で開いた二つ折りの紙の間に、開いた二つの面上にすべての頂点が乗るような多面体の折り紙押出成形を、立体ねじり折りの手法を用いて構成する。また応用例として、筒状に丸められる立体折り紙テセレーションを紹介する。
11:50-13:00	昼休み
13:00-13:20	ハンドル曲線を用いた曲線折り形状とその展開図の設計手法　瀬島青空、三谷純 Ohashiらは折り目の曲線と相似なハンドル曲線を用いることで、対話的に曲線折り形状を設計できることを示した。本研究ではハンドル曲線と対になる従ハンドル曲線を提案し、それらを同時に使用することで、ruling同士の交差が発生しないことを保証して曲線折りを設計できることを示す。また、この手法によって生じる展開図上の誤差について、最適化を用いた解決方法を新たに提案する。
13:20-13:40	ブロック折り紙の対話的設計支援システムの提案　遠藤匠、三谷純 一枚の紙を三角形の形状をしたブロックと呼ばれる単位に折り、複数個のブロックを組み上げることで作られる立体的作品をブロック折り紙と呼ぶ。本研究では、仮想空間上にブロックを配置することで対話的にブロック折り紙を設計できるシステムを提案する。提案システムでは、ブロックをバネ質点系モデルと見なしてシミュレーションを行うことで、ブロックに発生する物理的応力の再現を試みる。
13:40-13:55	ピンポイント除草のための軽量無反動アームの製作　柴﨑雄太 ドローンを用いた空中からのピンポイント除草は農薬使用の減少に有効だが、ドローンへのアーム実装は重量制限や反動の抑制などの制約により難しい。本研究では、Kresling構造を用いて紙を使用した軽量なアームを製作した。エンドエフェクタの自重で展開、ウィンチで収縮するアームである。また、側面の一部を切削することで風の通り道を作り、風の影響を小さくしている。この風の影響と展開に必要な最小の重量を実験により評価した。
13:55-14:10	四辺形境界モジュールを用いた変形する曲面の設計　田中一成、舘知宏 四辺形境界を持つ折紙構造「四辺形境界モジュール」の設計により、2つの与えられた境界形状の間を変形可能な機構が実現できることが知られている。本研究では、四辺形境界モジュールを連結することで、平面から任意の柱面へ変形する機構を設計する。また、四辺形境界モジュールを正対させ組み合わせて生まれる多安定構造についても検討する。
14:10-14:20	休憩
14:20-14:40	「創作折り紙」は吉澤章の造語か　松浦英子、木下芳夫 「創作折り紙」という用語は、現在は「新しく考え出した折り紙作品」という意味で一般に使われる言葉となっているが、1950年代に吉澤が自身の折り紙様式を表す言葉として使い始めたのではないかと考えられ、木下によれば、吉澤が最初に使ったのは1952年の『婦人公論』10月号であるという。本研究では、吉澤がどのようにこの用語を使って定義づけていたか、また吉澤の前後に活躍した作家たちの使用状況を調べた。
14:40-15:00	「一点刺し」課題の教材化に向けた基礎研究及び実践　烏山凌輔 一刀切りは、直線描画された任意の多角形の全ての辺を一直線上に折りたたむ課題である。ここで辺と頂点を入れ替えた「直線描画された任意の多角形の全ての頂点を一点に集められるか」という、いわば「一点刺し」なる課題を提案する。また、今後の教材化に向け、知的障害特別支援学級において授業実践を行った。生徒の反応や操作した折り紙を分析した上で、教材としての意義を述べる。
15:00-15:20	折り紙作家のニーズに合った形状設計手法の提案　内田 壮一郎 折り紙作品の創作を支援するTree Makerなどのソフトウェアは強力なツールである一方、実際に折り紙作家が創作活動で用いる機会は少ない。原因の１つとして、ソフトウェアで設計可能な形状が、作家のニーズを満たしきれていないことが挙げられる。これを解決するために、Tree MakerやOrigamizerをヒントにしながら、新しいアルゴリズムの研究を行っている。本発表では現在の進捗を報告する。
15:20-15:30	休憩
15:30-15:50	変形自由度の変化する折紙セル構造　安達瑛翔、十塚響、西本清里、割鞘奏太、野老朝雄、舘知宏 StroblによるSnapologyや野老によるBuildVoidを基に発想した、格子状に並ぶ立方体を正方形で繋いだ折紙セル構造を提案する。この構造は多くの変形モードを持ち、選んだモードにより変形自由度やポアソン比が変化する。二種類の変形モードをユニットごとに割当てる方法と、その割当による構造全体の自由度の切替について論じる。少し折れた状態で3Dプリントすることで変形モードを切替えることができた。
15:50-16:10	V-Fold Twister Mechanismを用いた双安定ポップアップシステムの提案　松田凌汰、舘知宏 V-Fold Twister Mechanismは、回転しながら展開する仕掛けとして、飛び出す絵本に用いられてきた。本発表ではこの仕掛けを複数連結して構築できる、線状に折りたたまれた状態から面状へと展開するポップアップシステムを提案し、これが双安定であることを解明する。さらに、これを積層させてできる立体へと展開するシステムや、ミウラ折りとの組み合わせ、Twisterの回転角を各々制御することで曲面化するシステムの設計手法についても紹介する。
16:10-16:30	曲線折紙ブロックを用いた軽量のモジュラー建設システム　Munkyun Lee, Mahmoud Abu-Saleem, Tomohiro Tachi, Joseph M. Gattas 本研究では曲線折紙の柱を用いて、迅速な軽量折紙建設システムを提案する。Elastica曲線に沿った曲面と台形の断面をもつ曲線折紙のブロックを設計し、そのブロックを互いにかみ合うように面接続することで連続的な壁面を建てる。生成文法を用いて多様な曲率の壁面を構築できることを示す。またデスクトップスケールと、実スケールのプロトタイプを示す。
16:30-17:00	飛び入り発表など

---

プラットフォーム

オンラインではZOOMを用います。各自ZOOMの環境をご用意ください。

---

主催

主催：日本折紙学会

協力：筑波大学　三谷研究室

---

過去の会など

こちらをごらんください。